Danger Den DD-M6 Waterblock Review

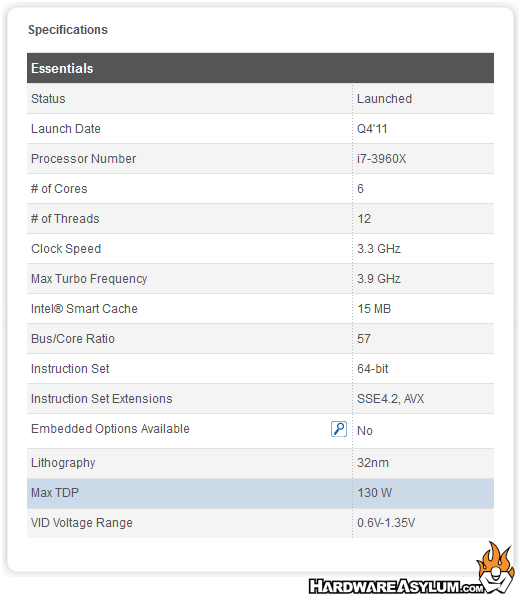
The Danger Den M6 waterblock is designed for all Intel Socket LGA2011 / 1366 / 1156 / 1155 processors.

Gigabyte X79 UD3 Intel X79 Chipset
Intel Core i7 3960X (3.3Ghz) Quad Core 4 x 256KB L2 Cache 8MB L3 Cache
Danger Den M6

Cooling Gear
Black Ice Triple 120mm radiator
Hydro L35 Pump

The CPUID System Monitor was used to obtain and record system temperature data and being that this is a quad core processor we need something that will work across all of the cores at once.  For this task we're using a new version of Prime95 (p95v255a) that will allow you to spawn (n) instances to test with.

Editors note: Even though the Windows 7 task manager reported 100% processor usage we could never attain a 100% of the rated heat output as documented by Intel (see below) when using Prime95 as a basis for that heat production. Knowing this we ran the stress test until the maximum temperature was attainted and stabilized.

Other things to consider when judging software induced heat output.
a) Clock throttling by the processor at high temperatures.
b) Normal software isn't designed to produce maximum heat output.
c) Variances of cooling temperature.
d) Variances in CPU load.
e) Inaccuracies in thermal diode readouts.
Of course the list goes on..

Our testing methodology is aimed to provide a real world look into this heatsink given the test system provided.

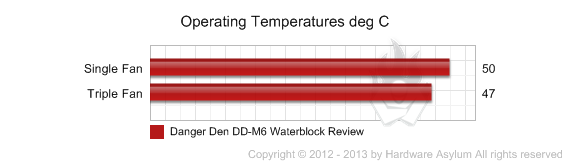
A C/W rating can quickly be calculated using this formula.

C/W = (CPU temp - Ambient temp)/(Variance(%) * CPU Watts)
Allowed variance for this test = 85%
CPU Watts = 130W

0.28 C/W = (50C - 19.2C)/(.85(130W))

For this next test the CPU speed was cranked up to 4.6Ghz and the test was re-run.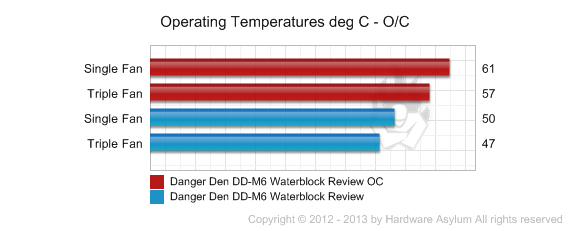

To calculate a new C/W rating for this test we will need to factor in the increased processor wattage. The formula and constants for this are listed below.

ocC/W = dCPU Watts * (ocMhz / dMhz) * (ocVcore / dVcore)2
ocMhz = 4600
dMhz = 3300
ocVcore = 1.2
dVcore = 1.35
The variance still applies for our C/W calculation
Allowed variance for this test = 85%
CPU Watts = 229W

0.21 C/W = (65C - 25.5C)/(.85(229W))

In our heatsink and waterblock tests we don't really focus on overall load temperatures but rather how well the product can remove heat given a specified heat load. Since this is a real world testing method we need to take into consideration real world variables and estimate tolerances. This is why we normally only apply 85% of the total wattage output to our heat calculations.

The resulting C/W number is used to rate how efficient a heatsink or waterblock is based on the given heat load. These numbers can be used to determine heat capacity, the larger the difference the less efficient the heatsink is. (aka not good for overclocking)

We are using the new Sandy Bridge E platform for these tests and you will notice that the total heat output is considerably higher than before on the order of the LGA1366.  During this test we were able to pump an estimated 229w of heat into the heatsink at 4.6Ghz and the results show it can handle a mild overclock quite well with only a ten degree delta.  In these tests you'll notice that the C/W numbers actually went down between the default and overclocked tests, which is something we normally see with watercooling and indicates we have yet to reach the thermal barrier with this cooling system.

It should also be noted that we did test this heatsink using two basic configurations.  The first was with only a single 120mm fan running on our triple fan radiator.  This is our normal configuration for motherboard reviews when we choose to watercool.  Just to see how the block would react we also spun up all three fans and noticed a four degree drop in overall temps.  

Keep in mind these calculations are provided for demonstration purposes only and may not reflect the actual lab tested C/W rating, but we're pretty close.